e2x次方的导数

踩死猪
2020-07-15
分享
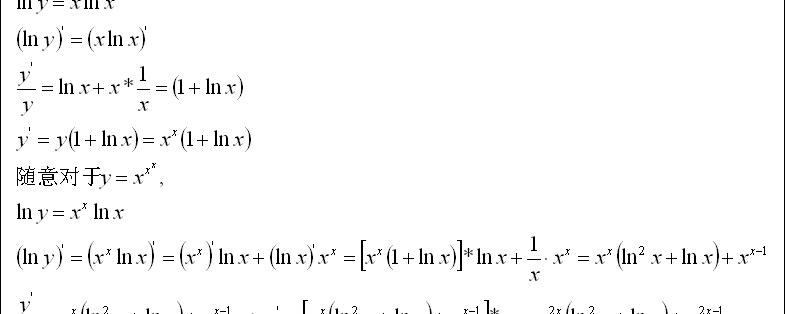
推荐回答

踩死猪
2022-01-19
e的2x次方的导数:2e^(2x)。
e^(2x)是一个复合函数,由u=2x和y=e^u复合而成。
计算步骤如下:
1、设u=2x,求出u关于x的导数u'=2;
2、对e的u次方对u进行求导,结果为e的u次方,带入u的值,为e^(2x);
3、用e的u次方的导数乘u关于x的导数即为所求结果,结果为2e^(2x)。
导数(Derivative),也叫导函数值,是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。
e^(2x)是一个复合函数,由u=2x和y=e^u复合而成。
计算步骤如下:
1、设u=2x,求出u关于x的导数u'=2;
2、对e的u次方对u进行求导,结果为e的u次方,带入u的值,为e^(2x);
3、用e的u次方的导数乘u关于x的导数即为所求结果,结果为2e^(2x)。
导数(Derivative),也叫导函数值,是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。
本网站引用、摘录或转载上述内容仅供网站访问者交流或参考,文中观点或信息与爱问公司无关,与之相关的任何事务以及法律责任均与爱问公司无关。
相关推荐
-
 英国哪些大学新闻传媒专业比较好英国新闻传媒专业比较好的大学,主要有以下:1、谢菲尔德大学;2、利兹大学;3、卡迪夫大学;4、诺丁汉特伦特大学;5、威斯敏斯特大学。等等。
英国哪些大学新闻传媒专业比较好英国新闻传媒专业比较好的大学,主要有以下:1、谢菲尔德大学;2、利兹大学;3、卡迪夫大学;4、诺丁汉特伦特大学;5、威斯敏斯特大学。等等。 -
 q5质量怎么样车是好车,舒适度方面,空间表现挺不错的,另外,配置方面,还是外国厂商一贯的作风,专门为中国消费者加装了非常多的舒适性方面的配置,具体的配置我就不罗列了。内饰,还是典型的家族风格,不张扬,但也不缺少惊喜,看上去非常不错,感觉很舒服,人机操作方面做的也不错,用料也都是上乘,可以放心。质量,没得说,豪华品牌,质量过硬是基础,要不然也不会叫豪华品牌。总的来说呢,这款车非常不错,特别是国产q5车型,搭载2.0t的发动机,而且是四驱,性价比还是挺高的,但是遗憾的是,需要加价买车,而且过分的是加价还要登上一年。替代车型,可以考虑沃尔沃xc60,宝马x3,都不错,不在q5之下的。
q5质量怎么样车是好车,舒适度方面,空间表现挺不错的,另外,配置方面,还是外国厂商一贯的作风,专门为中国消费者加装了非常多的舒适性方面的配置,具体的配置我就不罗列了。内饰,还是典型的家族风格,不张扬,但也不缺少惊喜,看上去非常不错,感觉很舒服,人机操作方面做的也不错,用料也都是上乘,可以放心。质量,没得说,豪华品牌,质量过硬是基础,要不然也不会叫豪华品牌。总的来说呢,这款车非常不错,特别是国产q5车型,搭载2.0t的发动机,而且是四驱,性价比还是挺高的,但是遗憾的是,需要加价买车,而且过分的是加价还要登上一年。替代车型,可以考虑沃尔沃xc60,宝马x3,都不错,不在q5之下的。  正时皮带做方向标记有什么用标方向标记的原因是防止装错方向,因为齿的方向磨损不同,如果装反了会减少正时皮带的寿命,严重的是如果皮带过早断掉会导致所有进气管断了,一根100,很合算
正时皮带做方向标记有什么用标方向标记的原因是防止装错方向,因为齿的方向磨损不同,如果装反了会减少正时皮带的寿命,严重的是如果皮带过早断掉会导致所有进气管断了,一根100,很合算-
 成都理工大学和浙江工业大学哪个好成都理工大学和浙江工业大学专业侧重不完全一样,严格来说没有什么可比性。非要比的话,成都理工大学有国家重点一级学科,入选了双一流,在本行业内的排名要比浙江工业大学好一些
成都理工大学和浙江工业大学哪个好成都理工大学和浙江工业大学专业侧重不完全一样,严格来说没有什么可比性。非要比的话,成都理工大学有国家重点一级学科,入选了双一流,在本行业内的排名要比浙江工业大学好一些 -
 怎样激发学困生的阅读兴趣培养阅读兴趣,刚开始可以选择喜欢的书籍阅读,这样不会导致你一来就产生讨厌的情绪。其次,给自己制定一个读书计划,养成读书的习惯。比如,一周读一本书,每天抽1-2个小时作为阅读时间。阅读的过程中或读后,要学会做一个简单的读书笔记,记录一下书籍、文章的:脉络主旨,主要人物以及事迹等以及阅读后的感悟,如果是学生还可以摘抄一些优美句子、段落等作为素材。读书笔记的用处是很大的,一方面是知识的积累,另一方面也可以培养你的阅读兴趣。另外,要掌握一个科学高效的阅读方法。无论是学生还是工作者,能够挤出来读书的时间总是有限的,所以一个高效的阅读方法很关键。我读书一般是用快速阅读法,这里说的快速阅读不是简单地阅读速度快,跟略读、跳读扫读等有着本质的区别。快速阅读是一种科学高效的阅读、学习方法。快速阅读不仅体现在阅读速度的高效上,更是理解的高效:对抓住文章段落的脉络和重点有非常好的作用,帮助我们对文章做整理、分析和归纳。具体练习可以参考《精英特全脑速读记忆软件》,用软件练习,每天一个多小时,一个月左右的练习可以提高阅读速度5倍左右、理解记忆也能得到相应的提高。我练习快速阅读,现在能做到一目三行(常规书籍排版)。掌握速读之后,可以把阅读效率提高好多倍,无论是阅读还是学习,都有极大的帮助的,如果你的阅读效率低,有必要练习提高一下。
怎样激发学困生的阅读兴趣培养阅读兴趣,刚开始可以选择喜欢的书籍阅读,这样不会导致你一来就产生讨厌的情绪。其次,给自己制定一个读书计划,养成读书的习惯。比如,一周读一本书,每天抽1-2个小时作为阅读时间。阅读的过程中或读后,要学会做一个简单的读书笔记,记录一下书籍、文章的:脉络主旨,主要人物以及事迹等以及阅读后的感悟,如果是学生还可以摘抄一些优美句子、段落等作为素材。读书笔记的用处是很大的,一方面是知识的积累,另一方面也可以培养你的阅读兴趣。另外,要掌握一个科学高效的阅读方法。无论是学生还是工作者,能够挤出来读书的时间总是有限的,所以一个高效的阅读方法很关键。我读书一般是用快速阅读法,这里说的快速阅读不是简单地阅读速度快,跟略读、跳读扫读等有着本质的区别。快速阅读是一种科学高效的阅读、学习方法。快速阅读不仅体现在阅读速度的高效上,更是理解的高效:对抓住文章段落的脉络和重点有非常好的作用,帮助我们对文章做整理、分析和归纳。具体练习可以参考《精英特全脑速读记忆软件》,用软件练习,每天一个多小时,一个月左右的练习可以提高阅读速度5倍左右、理解记忆也能得到相应的提高。我练习快速阅读,现在能做到一目三行(常规书籍排版)。掌握速读之后,可以把阅读效率提高好多倍,无论是阅读还是学习,都有极大的帮助的,如果你的阅读效率低,有必要练习提高一下。 -
 五羊本田125-m前脸有吗五羊本田125-M锋翔的前脸(头罩),到各地五羊本田专卖店就能买到,或者到某宝上搜“锋翔125导流罩”就能找到。
五羊本田125-m前脸有吗五羊本田125-M锋翔的前脸(头罩),到各地五羊本田专卖店就能买到,或者到某宝上搜“锋翔125导流罩”就能找到。 -
 数控车床fanucoi中的程序重启动怎么用程序重启一般是不用的该功能使用在加工过程中刀具损坏,突然停电等加工一半停止,可以使用该功能是程序从断电的地方起动,使用该功能要非常小心,控制不好容易出现撞刀等现象
数控车床fanucoi中的程序重启动怎么用程序重启一般是不用的该功能使用在加工过程中刀具损坏,突然停电等加工一半停止,可以使用该功能是程序从断电的地方起动,使用该功能要非常小心,控制不好容易出现撞刀等现象 -
 新摩托车骑几天之后就要清洗化油器吗?这种说法不正确,耗油大不是清不清洗的事。查一下是不是液化器的油针是不是高了。
新摩托车骑几天之后就要清洗化油器吗?这种说法不正确,耗油大不是清不清洗的事。查一下是不是液化器的油针是不是高了。 -
 新车要不要拉高速?要拉,2000就可以拉了,拉完动力和油耗都会有改善.建议拉后换高速,不过我上周去4s,4s人说拉完也不用换,因为明锐的都冷磨合过,里面比较感觉,即使拉了高速也不会太脏,可以首保再换,或5000公里去换
新车要不要拉高速?要拉,2000就可以拉了,拉完动力和油耗都会有改善.建议拉后换高速,不过我上周去4s,4s人说拉完也不用换,因为明锐的都冷磨合过,里面比较感觉,即使拉了高速也不会太脏,可以首保再换,或5000公里去换 -
 ufc是什么意思UFC中文意思是终极格斗冠军赛,是目前世界上最顶级和规模最庞大的职业MMA(综合格斗)赛事。每年举办超过20期,按次付费比赛直播,赛事擂台为标志性的八角笼,签约UFC的职业格斗选手都经过系统而科学的格斗训练,具备综合运用各种格斗技术的能力。UFC在1993年首办于美国丹佛,比赛擂台为标志性的八角笼,目的是在开放式规则下为不同武术流派的格斗家提供统一的竞技平台,从而产生终极冠军,原本只准备举办一届的赛事因超高的关注度延续了下来。
ufc是什么意思UFC中文意思是终极格斗冠军赛,是目前世界上最顶级和规模最庞大的职业MMA(综合格斗)赛事。每年举办超过20期,按次付费比赛直播,赛事擂台为标志性的八角笼,签约UFC的职业格斗选手都经过系统而科学的格斗训练,具备综合运用各种格斗技术的能力。UFC在1993年首办于美国丹佛,比赛擂台为标志性的八角笼,目的是在开放式规则下为不同武术流派的格斗家提供统一的竞技平台,从而产生终极冠军,原本只准备举办一届的赛事因超高的关注度延续了下来。 -
 汽车氧传感器注册商标属于哪一类?汽车氧传感器属于商标分类第12类1202群组;经路标网统计,注册汽车氧传感器的商标达9件。注册时怎样选择其他小项类:1.选择注册(陆地车辆用用离合器,群组号:1202)类别的商标有1件,注册占比率达11.11%2.选择注册(陆地车辆发动机,群组号:1202)类别的商标有1件,注册占比率达11.11%3.选择注册(陆地车辆刹车片,群组号:1202)类别的商标有1件,注册占比率达11.11%4.选择注册(利用汽车(ABS)防抱装置停车抱死装置,群组号:1202)类别的商标有1件,注册占比率达11.11%5.选择注册(陆地车辆刹车,群组号:1202)类别的商标有1件,注册占比率达11.11%6.选择注册(汽车轮胎压力报警装置,群组号:1202)类别的商标有1件,注册占比率达11.11%7.选择注册(汽车发动机电磁喷油器,群组号:1202)类别的商标有1件,注册占比率达11.11%8.选择注册(ABS防抱死装置(车辆刹车装置),群组号:1202)类别的商标有1件,注册占比率达11.11%9.选择注册(车辆防眩光装置,群组号:1202)类别的商标有1件,注册占比率达11.11%
汽车氧传感器注册商标属于哪一类?汽车氧传感器属于商标分类第12类1202群组;经路标网统计,注册汽车氧传感器的商标达9件。注册时怎样选择其他小项类:1.选择注册(陆地车辆用用离合器,群组号:1202)类别的商标有1件,注册占比率达11.11%2.选择注册(陆地车辆发动机,群组号:1202)类别的商标有1件,注册占比率达11.11%3.选择注册(陆地车辆刹车片,群组号:1202)类别的商标有1件,注册占比率达11.11%4.选择注册(利用汽车(ABS)防抱装置停车抱死装置,群组号:1202)类别的商标有1件,注册占比率达11.11%5.选择注册(陆地车辆刹车,群组号:1202)类别的商标有1件,注册占比率达11.11%6.选择注册(汽车轮胎压力报警装置,群组号:1202)类别的商标有1件,注册占比率达11.11%7.选择注册(汽车发动机电磁喷油器,群组号:1202)类别的商标有1件,注册占比率达11.11%8.选择注册(ABS防抱死装置(车辆刹车装置),群组号:1202)类别的商标有1件,注册占比率达11.11%9.选择注册(车辆防眩光装置,群组号:1202)类别的商标有1件,注册占比率达11.11% -
 白酒中的苦味放久会自己除掉吗白酒中的苦味放久不会自己除掉。白酒中的苦味,主要是因为酒中的醛类以及酚类化合物所导致的。因为粮食酒在酿造的过程当中,原料可能会出现一定的霉变现象,而且如果发酵池温度过高的话,也很容易会使白酒在酿造的过程当中出现苦味,而且像这种苦味一般来说是很难去除。
白酒中的苦味放久会自己除掉吗白酒中的苦味放久不会自己除掉。白酒中的苦味,主要是因为酒中的醛类以及酚类化合物所导致的。因为粮食酒在酿造的过程当中,原料可能会出现一定的霉变现象,而且如果发酵池温度过高的话,也很容易会使白酒在酿造的过程当中出现苦味,而且像这种苦味一般来说是很难去除。 -
 红毛丹发霉了可以吃吗红毛丹发霉了不可以吃。发霉了,外皮一定变黑了;里面的肉变得有点发黄了,而且味道也会变质。红毛丹又名毛荔枝,现代营养学研究发现它含有丰富的钙质、磷、维他命C。熟果的颜色呈鲜红色或略带黄色。
红毛丹发霉了可以吃吗红毛丹发霉了不可以吃。发霉了,外皮一定变黑了;里面的肉变得有点发黄了,而且味道也会变质。红毛丹又名毛荔枝,现代营养学研究发现它含有丰富的钙质、磷、维他命C。熟果的颜色呈鲜红色或略带黄色。 -
 大家觉得卡罗拉和雷凌哪款比较好?个人感觉雷凌好。首先是外观,雷凌要更时尚运动一些,然后是空间,两车差不多,但是雷凌后排空间要大一些,再说发动机,雷凌畅销款1.6自动精英版是原装进口发动机,雷克萨斯技术,最后雷凌有现车,卡罗拉需要等。价位,配置差不多,价格卡罗拉要贵5000左右。综合考虑雷凌,你值得拥有
大家觉得卡罗拉和雷凌哪款比较好?个人感觉雷凌好。首先是外观,雷凌要更时尚运动一些,然后是空间,两车差不多,但是雷凌后排空间要大一些,再说发动机,雷凌畅销款1.6自动精英版是原装进口发动机,雷克萨斯技术,最后雷凌有现车,卡罗拉需要等。价位,配置差不多,价格卡罗拉要贵5000左右。综合考虑雷凌,你值得拥有 -
 吉利远景机器缸压不够怎么办把缸压比作一个小盒子,只允许一点点汽油进入这盒子,这时有火花出现,就会点燃着火,是因为气油浓度到了能着火的程度,但同样多的一点点汽油进入一个大些盒子,这时点火就不会点燃,因为大盒子的汽油浓度达不到着火
吉利远景机器缸压不够怎么办把缸压比作一个小盒子,只允许一点点汽油进入这盒子,这时有火花出现,就会点燃着火,是因为气油浓度到了能着火的程度,但同样多的一点点汽油进入一个大些盒子,这时点火就不会点燃,因为大盒子的汽油浓度达不到着火 -
 双离合啥意思 啥作用双离合其实也是自动挡,在机械结构上更像手动挡的变速箱通过各种电子和机械装置控制两组离合器。除了拥有手动变速器的灵活性及自动变速器的舒适性外还能提供无间断的动力输出。
双离合啥意思 啥作用双离合其实也是自动挡,在机械结构上更像手动挡的变速箱通过各种电子和机械装置控制两组离合器。除了拥有手动变速器的灵活性及自动变速器的舒适性外还能提供无间断的动力输出。 -
 吉祥狮电动车,大龟王型号要多少钱啊不带电池2600是差不多带了电池的话,怎么都要3300左右我的买来2950认识的。。。
吉祥狮电动车,大龟王型号要多少钱啊不带电池2600是差不多带了电池的话,怎么都要3300左右我的买来2950认识的。。。 -
 12年别克2,4L7座卖多少钱商务车?不知车况,不知公里数......................估价十一万到十三万吧。
12年别克2,4L7座卖多少钱商务车?不知车况,不知公里数......................估价十一万到十三万吧。 -
 凯立德导航现在改名了吗没有呀,还是凯立德也许你是看到“凯行”了吧?那是一个车联网项目
凯立德导航现在改名了吗没有呀,还是凯立德也许你是看到“凯行”了吧?那是一个车联网项目


 微信
微信
 微博
微博
 QQ空间
QQ空间
 复制网址
复制网址
